Esercizi di Statistica Descrittiva Unidimensionale: Frequenze, Media e Misure di Posizione
Classificato in Matematica
Scritto il in  italiano con una dimensione di 23,13 KB
italiano con una dimensione di 23,13 KB
Statistica Descrittiva Unidimensionale: Frequenze e Rappresentazione Grafica
Esercizio 1: Numero di persone per nucleo familiare
Quando abbiamo chiesto a 20 individui il numero di persone che vivono in casa, abbiamo ottenuto le seguenti risposte:

- Costruire una **tabella di frequenze assolute e relative**.
- Rappresentare graficamente la distribuzione (utilizzando le **frequenze assolute**).
Soluzione:
a)

b)

Esercizio 2: Numero di telefoni per abitazione
In una compagnia telefonica sono interessati a conoscere il numero di telefoni (compresi i telefoni cellulari) presenti nelle case. È stato condotto un sondaggio e finora sono state ricevute le seguenti risposte:

- Costruire una **tabella di frequenze assolute e relative**.
- Rappresentare graficamente la distribuzione (utilizzando le **frequenze assolute**).
Soluzione:
a)

b)

Esercizio 3: Risposte corrette in un test
In una classe è stato somministrato un test a scelta multipla di 40 domande. Il numero di risposte corrette realizzate da ciascuno degli studenti è il seguente:

- Riassumere i dati utilizzando una **tabella di frequenze assolute e relative**.
- Rappresentare graficamente questa distribuzione (utilizzando le **frequenze assolute**).
Soluzione:
a)

b)

Esercizio 4: Giorni dedicati allo sport
Abbiamo chiesto a 20 persone il numero medio di giorni alla settimana in cui fanno sport e abbiamo ottenuto le seguenti risposte:

- Costruire una **tabella di frequenze assolute e relative**.
- Rappresentare graficamente la distribuzione (utilizzando le **frequenze assolute**).
Soluzione:
a)

b)

Esercizio 5: Lancio di un dado
Abbiamo lanciato un dado 20 volte e abbiamo registrato i risultati:

- Ordinare i dati in una **tabella di frequenze assolute e relative**.
- Rappresentare graficamente la distribuzione (utilizzando le **frequenze assolute**).
Soluzione:
a)

b)

Esercizio 6: Tempi in uno sprint (Dati raggruppati)
In uno sprint è stato cronometrato il tempo impiegato da ogni partecipante per percorrere una distanza fissa. I tempi, indicati in secondi, sono i seguenti:

- Costruire una **tabella di frequenza**, raggruppando i dati in **intervalli di ampiezza 1**, a partire da 8.
- Rappresentare graficamente la **distribuzione**.
Soluzione:
a)
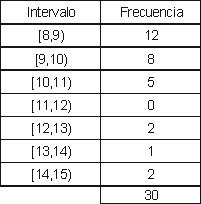
b)

Esercizio 7: Ore di studio settimanali
In una classe è stato chiesto agli studenti il numero di ore trascorse a settimana a studiare. Le risposte sono state le seguenti:
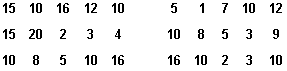
- Ordinare i dati in una **tabella di frequenze**, raggruppandoli in **intervalli di ampiezza 3**, a partire da 0.
- Rappresentare graficamente la **distribuzione**.
Soluzione:
a)
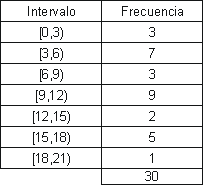
b)

Esercizio 8: Altezza di 30 persone
Abbiamo misurato l'altezza in centimetri di 30 persone, con i seguenti risultati:

- Costruire una **tabella di frequenza**, raggruppando i dati in **intervalli di ampiezza 5**, con inizio a 146,5.
- Rappresentare graficamente la **distribuzione**.
Soluzione:
a)
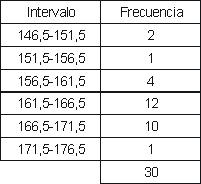
b)

Esercizio 9: Età di un gruppo di 30 persone
In un gruppo di 30 persone è stata registrata l'età di ciascuno, ottenendo i seguenti dati:

- Costruire una **tabella di frequenza**, raggruppando i dati in **intervalli di ampiezza 5**, a partire da 0.
- Rappresentare graficamente la **distribuzione**.
Soluzione:
a)

b)

Esercizio 10: Peso di 30 bambini
Un esame medico è stato condotto su un gruppo di 30 bambini. Uno dei dati rilevati è stato il peso in chilogrammi di ciascuno, con i seguenti risultati:

- Costruire una **tabella di frequenza**, raggruppando i dati in **intervalli di ampiezza 3**, a partire da 24,5.
- Rappresentare graficamente la **distribuzione**.
Soluzione:
a)

b)
Calcolo di Media e Deviazione Standard
Esercizio 11: Voti in un test di matematica
I voti ottenuti in un test di matematica sono elencati nella seguente tabella:

- Trovare la **media** e la **deviazione standard**.

Soluzione:
a)

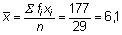

Il **punteggio medio** della classe è **6,1**, con una **deviazione standard** di 2,27.

Esercizio 12: Tempo di percorrenza casa-bus
Su uno scuolabus è stato chiesto agli studenti il tempo necessario per arrivare da casa alla fermata del bus. I risultati sono riportati nella tabella seguente:

Calcolare la **media** e la **deviazione standard** di questa distribuzione.
Soluzione:
Abbiamo trovato il **valore centrale** (o marchio di classe), x me, per ogni intervallo e preparato la tabella:
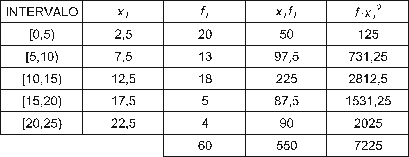


Gli studenti impiegano, in media, **9,17 minuti**, con una **deviazione standard** di 6,03 minuti.
Esercizio 13: Composizione del nucleo familiare
Quando è stato chiesto a 50 famiglie il numero di persone che compongono il nucleo familiare, abbiamo ottenuto le informazioni contenute nella tabella seguente:

- Trovare la **media** e la **deviazione standard**.

Soluzione:
a)

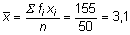

Il **numero medio** di persone che formano il nucleo familiare è **3,1**, con una **deviazione standard** di 1,1 persone.

Esercizio 14: Media e Deviazione Standard per distribuzione d'età
Trovare la **media** e la **deviazione standard** per la distribuzione d'età:

Soluzione:
Abbiamo trovato il **valore centrale** (o marchio di classe), x me, per ogni intervallo e preparato la tabella:



L'**età media** è **15,5 anni** con una **deviazione standard** di 6,71 anni.
Esercizio 15: Lancio di un dado (100 volte)
Abbiamo lanciato un dado 100 volte, registrando il risultato ogni volta. Le informazioni sono riportate nella seguente tabella:

- Trovare la **media** e la **deviazione standard**.

Soluzione:
a)

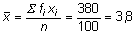

Abbiamo ottenuto un **punteggio medio** di **3,8**, con una **deviazione standard** di 1,75 punti.

Misure di Dispersione Relativa: Coefficiente di Variazione
Esercizio 16: Confronto tra classi A e B
Il voto medio della classe A in un test è stato di **5,5**, con una deviazione standard di **2,1**. In un'altra classe, B, il voto medio nella stessa prova è stato di **7,3** e la deviazione standard di **2,6**. Calcolare il **coefficiente di variazione** e confrontare la dispersione di entrambi i gruppi.
Soluzione:

Esercizio 17: Confronto salariale tra aziende A e B
Il salario medio dei lavoratori di una società, A, è di **900 euro** al mese, con una deviazione standard di **100 euro**. In un'altra azienda, B, lo stipendio medio è di **980 €** al mese con una deviazione standard di **150 euro**. Calcolare il **coefficiente di variazione** e indicare quale delle due aziende presenta una maggiore variazione relativa dei salari.
Soluzione:

Esercizio 18: Confronto di peso tra specie animali A e B
Il peso medio di una specie animale, A, è **21,3 kg** e la deviazione standard è di **2,5 kg**. In un'altra specie animale, B, il peso medio è di **125 kg** e la deviazione standard è di **13 kg**. Calcolare il **coefficiente di variazione** e indicare quale delle due specie presenta una maggiore variazione relativa nei pesi.
Soluzione:

Misure di Posizione: Mediana, Quartili e Percentili
Esercizio 19: Libri acquistati in libreria
In una libreria è stato registrato il numero di libri acquistati da ogni persona che è entrata nel negozio. La tabella seguente riassume le informazioni:

Calcolare la **Mediana** (I), il **Primo Quartile** (Q 1), il **Terzo Quartile** (Q 3) e l'**Ottantesimo Percentile** (P 80).
Soluzione:
Costruiamo la **tabella di frequenza cumulativa**:


Il **50%** delle persone ha comprato 2 libri o meno, e il restante 50% ha acquistato 2 o più libri. Interpretando allo stesso modo:

Esercizio 20: Lancio di una moneta (Numero di lanci prima della prima testa)
Abbiamo lanciato una moneta e registrato il numero di lanci necessari per ottenere la prima "testa". Abbiamo condotto l'esperimento 100 volte, con i seguenti risultati:

Calcolare la **Mediana** (I), il **Primo Quartile** (Q 1), il **Terzo Quartile** (Q 3) e il **Trentesimo Percentile** (P 30).
Soluzione:
Costruiamo la **tabella di frequenza cumulativa**:


Il **50%** delle volte abbiamo ottenuto 2 o meno lanci, e il restante 50% ha richiesto 2 o più lanci. Interpretando allo stesso modo:

Esercizio 21: Risultati del lancio di un dado (120 volte)
Nella tabella seguente abbiamo riassunto i risultati ottenuti lanciando un dado 120 volte:

Calcolare la **Mediana** (I), il **Primo Quartile** (Q 1), il **Terzo Quartile** (Q 3) e il **Ventesimo Percentile** (P 20).
Soluzione:
Costruiamo la **tabella di frequenza cumulativa**:


Il **50%** delle volte è stato ottenuto un punteggio inferiore o uguale a 3, e il 50% delle volte è stato ottenuto un punteggio maggiore o uguale a 3. Interpretando allo stesso modo:

Esercizio 22: Punteggi in un evento sportivo
Un gruppo di atleti ha ottenuto i seguenti punteggi in un evento sportivo valutato da 0 a 5 punti:

Calcolare la **Mediana** (I), il **Primo Quartile** (Q 1) e il **Terzo Quartile** (Q 3).
Soluzione:
Costruiamo la **tabella di frequenza cumulativa**:


Il **50%** degli atleti ha ottenuto un punteggio uguale o inferiore a 4, e il 50% ha ottenuto un punteggio pari o superiore a 4. Interpretando allo stesso modo:

Esercizio 23: Calcolo di Mediana, Quartili e Percentile (Dati raggruppati)
Calcolare la **Mediana** (I), il **Primo Quartile** (Q 1), il **Terzo Quartile** (Q 3) e il **Novantesimo Percentile** (P 90) per la seguente distribuzione:

Soluzione:
Costruiamo una **tabella di frequenza cumulativa**:



